63. 不同路径 II

发表于 | 分类于 | 阅读次数：

链接：https://leetcode-cn.com/problems/unique-paths-ii/

题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？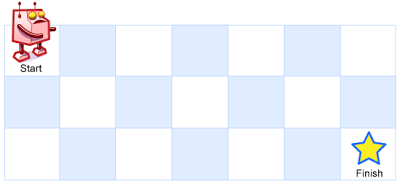
Alt text

网格中的障碍物和空位置分别用 1 和 0 来表示。
说明：m 和 n 的值均不超过 100。
示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

分析

本题接上一题62题，稍作修改，加入障碍物的判断，即可解决。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid) -> int:
        n = len(obstacleGrid)
        if n == 0:
            return 0
        m = len(obstacleGrid[0])
        if obstacleGrid[0][0] == 1:
            return 0
        dp = [[0] * m for _ in range(n)]
        dp[0][0] = 1
        for step in range(1, m + n - 2 + 1):
            max_y = min(step + 1, m)
            for y in range(max_y):
                x = step - y
                if x > n - 1:
                    continue
                if obstacleGrid[x][y] == 1:
                    dp[x][y] = 0
                    continue
                nums = 0
                if 0 <= x - 1 <= n - 1:
                    nums += dp[x - 1][y]
                if 0 <= y - 1 <= m - 1:
                    nums += dp[x][y - 1]
                dp[x][y] = nums
        return dp[n - 1][m - 1]

调优

但是这种算法时间复杂度并不好。我们来进行适当的优化。
我们会发现，只有边界的行列只依赖于前一个元素，剩下所有的行列都是依赖于相邻的两个元素。所以我们可以先把边界算出来，再算其他的。具体算法为：

  1. 如果第一个格点 obstacleGrid[0,0] 是 1，说明有障碍物，那么机器人不能做任何移动，我们返回结果 0。否则，如果 obstacleGrid[0,0] 是 0，我们初始化这个值为 1 然后继续算法。
  2. 遍历第一行，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i,j-1]。
  3. 遍历第一列，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i-1,j]。
  4. 现在，从 obstacleGrid[1,1] 开始遍历整个数组，如果某个格点初始不包含任何障碍物，就把值赋为上方和左侧两个格点方案数之和 obstacleGrid[i,j] = obstacleGrid[i-1,j] + obstacleGrid[i,j-1]。
  5. 如果这个点有障碍物，设值为 0 ，这可以保证不会对后面的路径产生贡献。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid) -> int:
        n = len(obstacleGrid)
        if n == 0:
            return 0
        m = len(obstacleGrid[0])
        if obstacleGrid[0][0] == 1:
            return 0
        obstacleGrid[0][0] = 1
        # 先计算第0行
        for j in range(1, m):
            if obstacleGrid[0][j] == 1:
                obstacleGrid[0][j] = 0
            else:
                obstacleGrid[0][j] = obstacleGrid[0][j - 1]
        # 再计算第0列
        for i in range(1, n):
            if obstacleGrid[i][0] == 1:
                obstacleGrid[i][0] = 0
            else:
                obstacleGrid[i][0] = obstacleGrid[i - 1][0]
        # 然后计算剩下所有的
        for i in range(1, n):
            for j in range(1, m):
                if obstacleGrid[i][j] == 1:
                    obstacleGrid[i][j] = 0
                else:
                    obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1]
        return obstacleGrid[n - 1][m - 1]

复杂度分析

  • 时间复杂度 ： $O(M \times N)$。长方形网格的大小是 $M \times N$，而访问每个格点恰好一次。
  • 空间复杂度 ： $O(1)$。我们利用 obstacleGrid 作为 DP 数组，因此不需要额外的空间。

可以看到效果是非常不错的！

Alt text